激活函数是一种添加到人工神经网络中的函数,旨在帮助网络学习数据中的复杂模式。在神经网络中,一个节点的激活函数定义了该节点在给定输入或输入集合下的输出。
激活函数的作用:
神经网络中每一层的输入输出都是一个线性求和的过程,如果没有(非线性)激活函数,那么无论构造的神经网络有多么复杂,有多少层,最后的输出都是输入的线性组合。纯粹的线性组合不能解决复杂问题,而引入了非线性激活函数以后,神经网络可以逼近任何非线性函数,从而处理更加复杂的问题。
梯度消失问题:
有些神经元的梯度趋近于0,这些神经元的权重不会更新,也被称为饱和神经元。此外,与饱和神经元相连的神经元的权重也会更新的很慢。如果神经网络中包含大量的饱和神经元,那么这个网络无法进行反向传播,这一问题就是梯度消失。
Sigmoid激活函数
Sigmoid函数也叫Logistic函数,该函数将一个实数映射到(0,1)的区间,可以用来做二分类。
该函数的优点:
- 由于输出范围是
(0,1),该激活函数对每个神经元的输出进行了归一化 - 和概率的取值范围一样,适合将预测概率作为输出的模型
- 函数可微且梯度平滑,避免出现跳跃的输出值
该函数的缺点:
- 函数趋于0或者1的时候,函数的梯度趋近于0,可能会导致梯度消失
- 输出不以零为中心,会导致后一层的神经元输入发生偏置偏移(Bias Shift),进而使得梯度下降收敛速度变慢
- 指数计算成本较高,影响运行速度
Tanh激活函数
Tanh激活函数又叫做双曲正切激活函数,与Sigmoid函数类似,但是Tanh函数的输出以零为中心,输出范围是(-1, 1)。
该函数的优点:
- 相较于Sigmoid函数,Tanh函数的输出是以零为中心的,这意味着正负值的分布是均匀的,有助于数据在训练过程中保持稳定,也有助于加速收敛
- 虽然在输入值过大或过小时,梯度接近于0,但是相较于Sigmoid函数,Tanh函数的中间区域的梯度更大,可以一定程度上缓降梯度消失问题
该函数的缺点:
- 输入较大或者较小时,输出几乎是平滑的且梯度较小,不利于权重更新,仍然存在梯度消失问题
- 指数计算需要更多资源
ReLU激活函数
ReLU函数又称为修正线性单元(Rectified Linear Unit),是一种分段线性函数。
该激活函数的优点:
- 输入为正时,导数为1,一定程度上改善了梯度消失问题,加速梯度下降的收敛速度
- 只存在线性关系,计算速度很快
- 有一定的生物学合理性,如单侧抑制
该激活函数的缺点:
- 当输入为负时,输出为0,反向传播时可能会导致梯度消失
- 不以零为中心,会给下一层神经元引入偏置偏移,影响梯度下降的效率
Leaky ReLU激活函数
该函数是对ReLU激活函数的优化,主要解决ReLU激活函数中梯度消失的问题。
其中$\gamma$是个很小的数,如0.1或者0.01等。
该激活函数的优点:
- 允许负值以小斜率通过,有助于避免神经元失活,使得模型更容易学习
- 具有ReLU函数的优点
该激活函数的缺点:
- 负斜率是一个超参数,如何选择该参数需要通过实验来确定,设置过大会导致模型过拟合,设置过小又无法充分发挥Leaky ReLU的优势
- 梯度的反向传播不如ReLU稳定,会导致训练过程中出现波动
ELU激活函数
ELU,全称是Exponential Linear Unit,该激活函数同样是针对ReLU负数部分存在的问题,被证实有较高的噪声鲁棒性。
该激活函数的优点:
- ELU在输入值非常小的时候,会饱和至负值,具有一定的鲁棒性
- 避免“死亡ReLU”问题
该激活函数的缺点:
- 涉及指数计算,其计算复杂度相对较高,导致训练大型神经网络时训练速度较慢
- 在输入较小时,梯度可能会饱和,导致训练的某些阶段权重更新缓慢,影响模型收敛速度
Softmax激活函数
Softmax激活函数主要用于多分类问题的输出层,将神经网络的输出转换为概率分布。
该激活函数的优点:
- 能够将神经网络的输出转换为概率分布,非常适用于多分类任务
该激活函数的缺点:
- 当输入值非常大或者非常小的时候,Softmax函数的梯度会变得很小,可能会导致梯度消失问题,影响模型的训练效果
- Softmax函数计算时涉及指数运算,可能会增加计算复杂度
一般来说,Softmax函数用于单标签的多分类问题,即每个样本只能属于一个类别。如果是多标签的多分类任务,即每个样本可能属于多个类别,那么使用Sigmoid激活函数更为合适,因为该激活函数将每个类别的输出独立地映射到(0,1)之间,从而允许每个样本属于多个类别。
GeLU激活函数
GeLU全称是Gaussian Error Linear Unit,其在激活中引入了随机正则的思想,是一种对神经元输入的概率描述。GeLU直观上更符合自然认知,同时实验效果要比ReLU和ELU要好,在Transformer模型中表现优异,能够避免梯度消失问题。
其中$\Phi(x)$是$x$的正态分布的累积函数。由于这个累积函数无法直接计算,研究者在研究过程中发现GeLU激活函数可以被近似地表示为:
或者:
该激活函数的图像为:
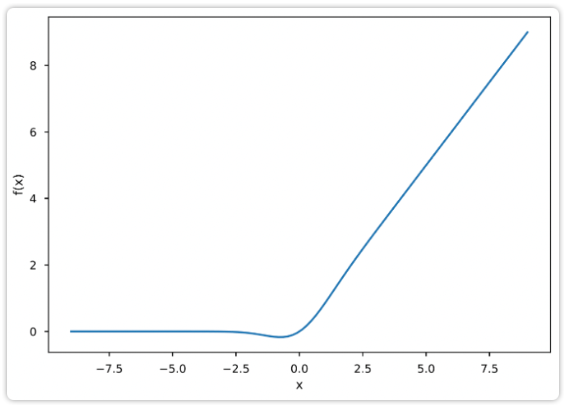
该激活函数的优点:
- 对于比较大的输入($x>0$),GeLU基本上是线性输出,和ReLU类似
- GeLU函数是处处连续,光滑可导的,在负值区域不再全为0,解决了Dead ReLU问题
- GeLU具有自归一化的性质,这意味着它在训练过程中可以帮助稳定神经网络的梯度,有助于加速收敛
该激活函数的缺点:
- GeLU的计算要比传统的ReLU激活函数要复杂,虽然可以通过近似方法来简化计算,但是仍然增加了计算成本
- 在某些情况下,GeLU可能会增加模型的内存需求
Swish激活函数
Swish激活函数的计算方式如下:
该激活函数的图像为:
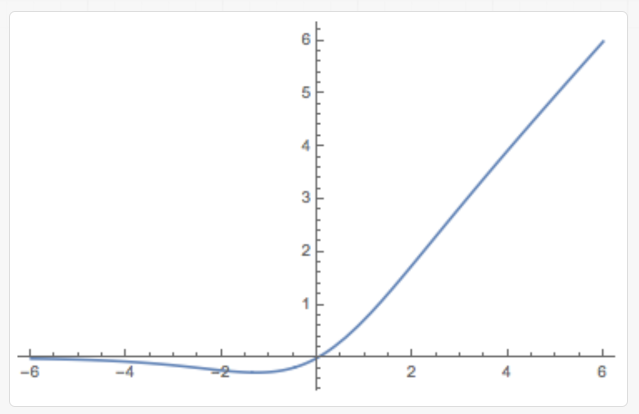
该激活函数的优点:
- Swish激活函数是一个非单调函数,它能够帮助模型捕获更复杂的数据特征,提升模型性能
- Swish函数及其导数都是平滑的,有助于提高梯度下降的效率
该激活函数的缺点:
- Swish的计算成本要比ReLU等简单激活函数要高
SwiGLU激活函数
计算公式如下:
GeGLU激活函数
计算公式如下:
经典开源模型使用的激活函数:
| Model | 激活函数 |
|---|---|
| GPT3 | GeLU |
| Llama | SwiGLU |
| Llama2 | SwiGLU |
| baichuan | SwiGLU |
| ChatGLM-6B | GeLU |
| ChatGLM2-6B | SwiGLU |
【参考文献】